La segunda ola

Las medidas de “distanciamiento social” tomadas para disminuir los contactos de personas “susceptibles” con “contagiosos” (directos o a través de objetos que se toquen) son efectivas para reducir el crecimiento de los contagios, pero tienen consecuencias segundarias graves en la vida cotidiana de las personas y en la economía. Por lo cual hay presión para “desconfinar” lo más ante posible. Un ejemplo de esto es la idea que tiene el Ministro de Educación de volver a operaciones escolares “normales” a partir de la última semana de abril.

Otras voces dan a pensar que esto – si se hace demasiado temprano – podría resultar en una “segunda ola”. ¿Qué hay con esto de una “segunda ola”? ¿Cómo saber qué es “demasiado temprano”?

Usando el modelo de simulación (más info sobre el modelo), he comparado el escenario de base (lo que habría pasado sin “distanciamiento”), una reducción drástica de los contactos durante 180 días y la misma reducción pero solo hasta el día 98 (ver también el video sobre estas simulaciones).

Todas las simulaciones usan un número básico de reproducción de 5,7 (número de personas que un infeccioso puede contagiar en total), un periodo de recuperación de 5,7 días (tomando en cuenta los diferentes desarrollos de la infección con el respectivo peso del grupo poblacional), y entonces inicialmente, cada infectuoso puede contagiar 1 susceptible por día. El primer escenario no cambia esto, y produce los resultados siguientes:

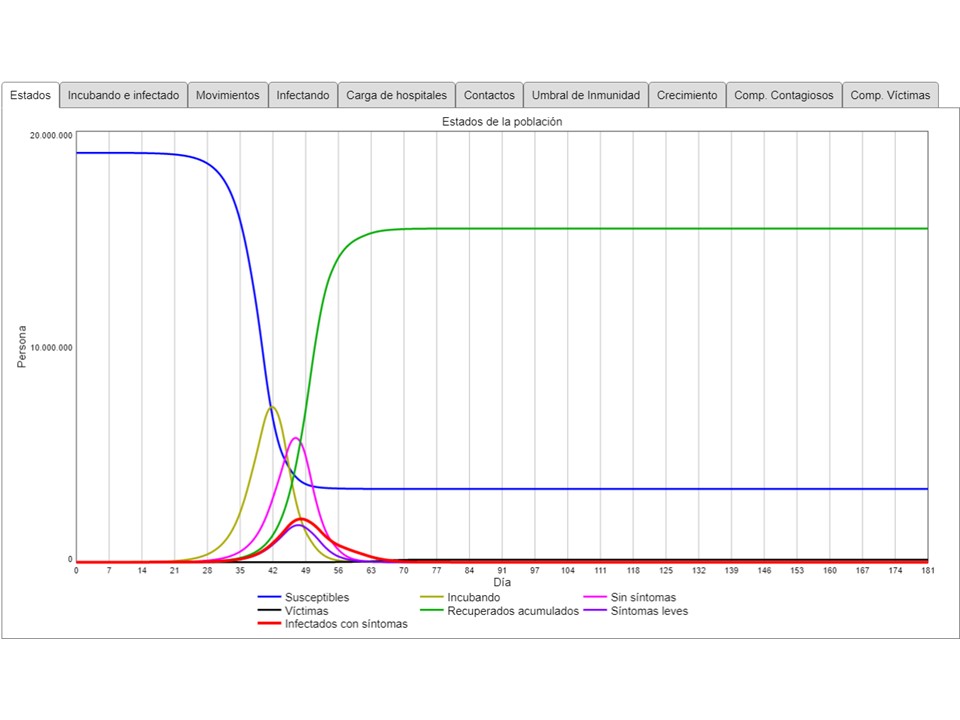
Los susceptibles disminuyen rapidamente durante las semanas 4-8, quedando a unos 18% de la población total (debido al umbral de inmunidad de grupo que se discute más bajo), y los recuperados devienen el prupo mayor de la población. Los estados intermedios de la epidemia – incubando e infectado – tienen sus respectivo “peak” en estas semanas:

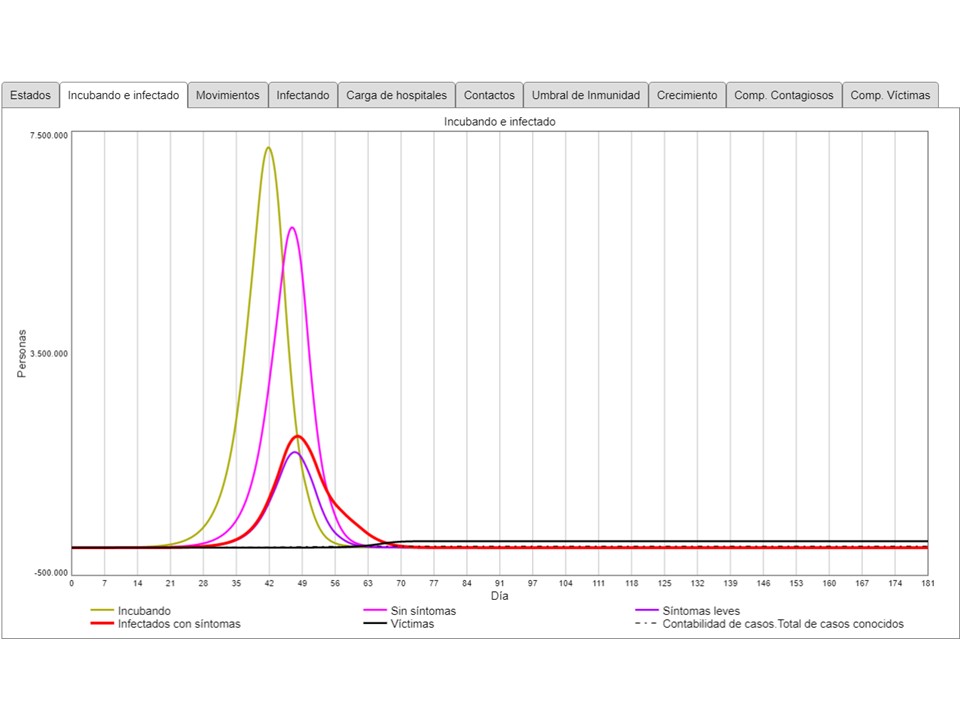
En el momento más fuerte, habrá caso 7,5 millones de personas en la fase de incubación. 1 a 2 semanas más tarde ocurre el “peak” de los asintomáticos y de los sintomáticos (levemente más tarde porque los síntomas más graves surgen unos días después de los primeros síntomas). Serán alrededor de 2 millones de infectados con síntomas (sin poner mucha enfasis en la precisión numérica: es un modelo muy simplificado y con muchos supuestos alimentados desde lo que los centros de control de epidemias publican).

En segundo escenario usa una reducción de los contactox críticos por día desde 1 a 0,3 desde el 20 de marzo con 5 días de puesta en marcha, y la restricción se mantiene durante los 180 días simulados:

La transición de susceptible a recuperado es diferente en varios aspectos: ocurre más tarde (semanas 8-16), toma más tiempo, los susceptibles permanecen la mayoría y los “peak” de los estados intermedios son menos altos:

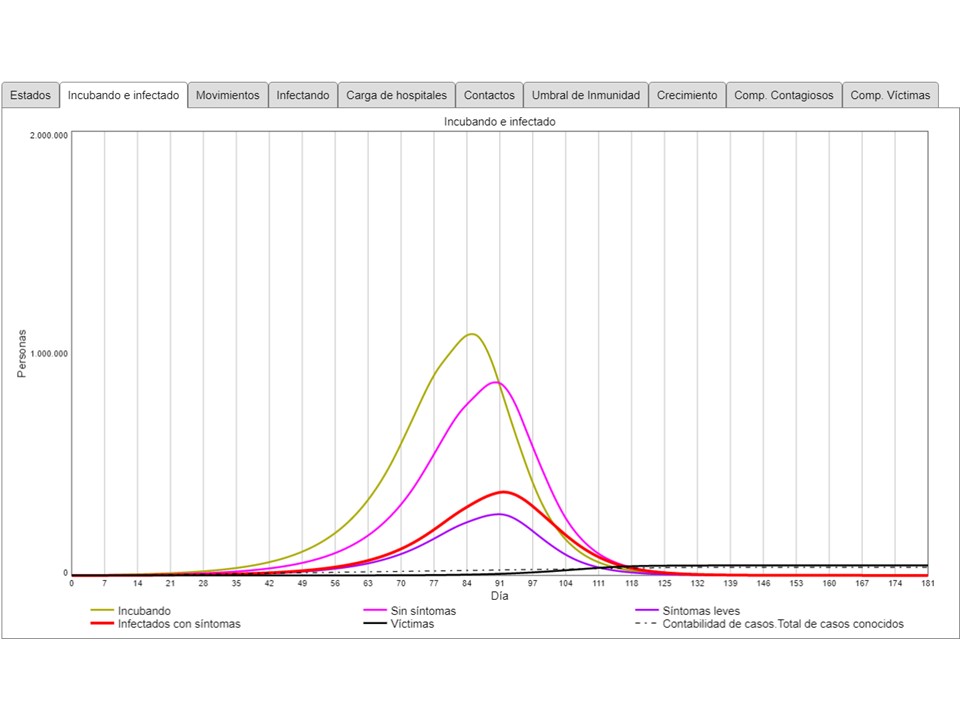
En comparación con el primer escenario, son solo 1 millón incubando, y alrededor de 400 mil infectados con síntomas. Esta última diferencia es muy visible cuando se compara el total de contagiosos (los infectados más los incubando en su último día de incubación):

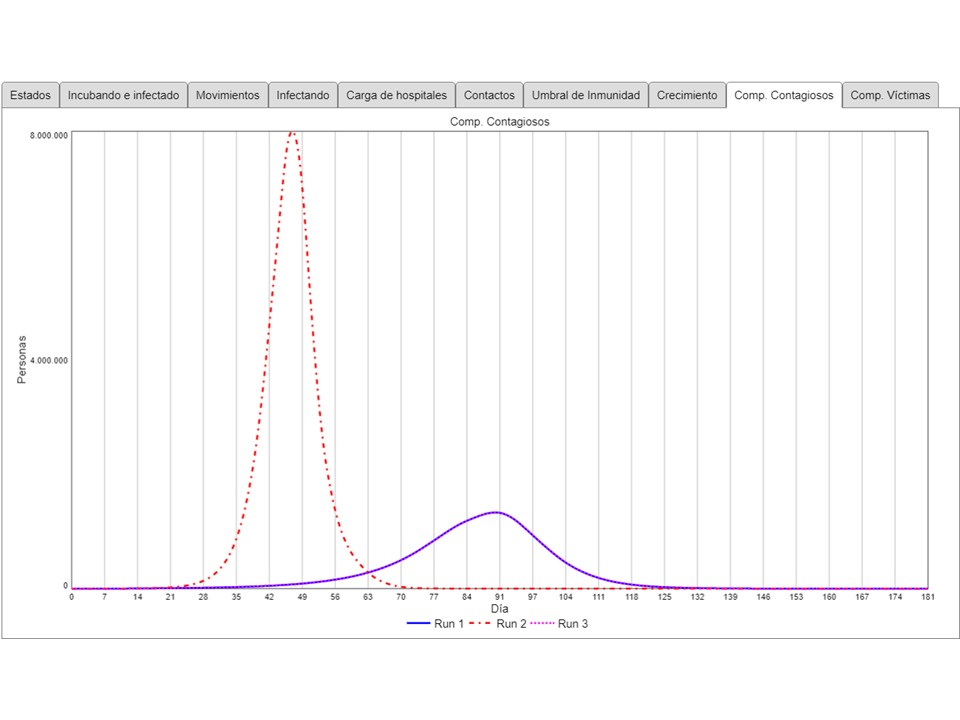
Esto es lo que se esperaba lograr con el “distanciamiento”. Entonces seguramente alrededor del día 100, ¿se podría levantar la medida de restricción sin correr riesgos?

Esto es lo que simula el tercer escenario: la medida se toma igual que en el segundo escenario, pero el día 98 se levanta. El resultado es una discontinuidad en las curvas de los susceptibles y de los recuperados:

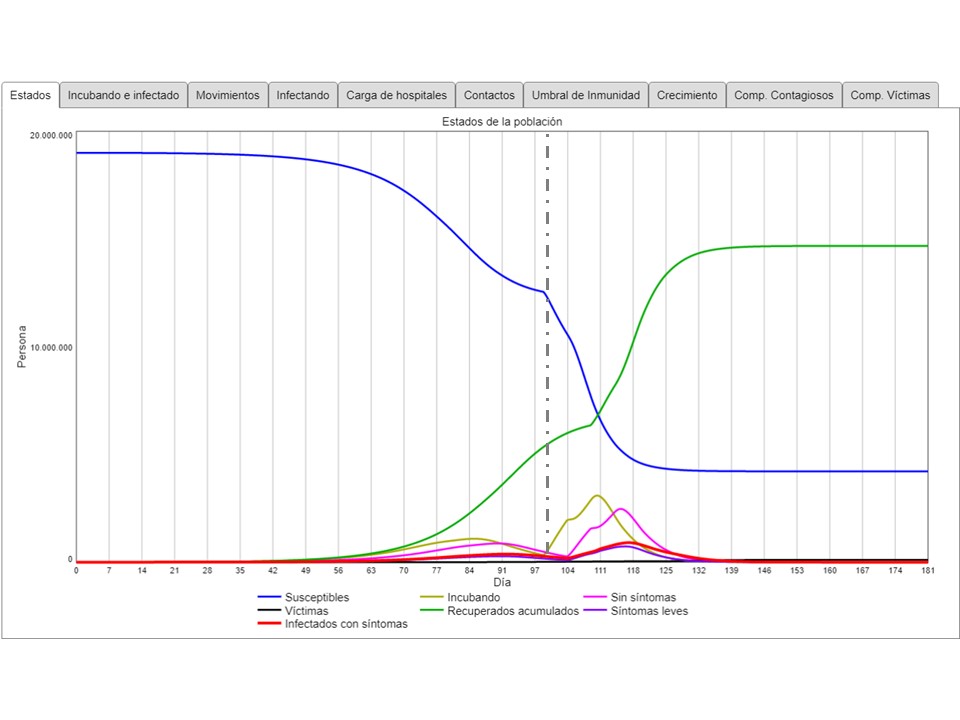
Cuando se levanta la restricción, sube instantáneamente el número de personas en la fase de incubación (lo que resta susceptibles), seguido por el mismo ascenso de los infectados (asintomáticos primero, sintomáticos después) y finalmente hay mucho más personas llegando al estado de recuperado. Al observar solo los grupos en los estados intermedios, se ven las dos “olas”:

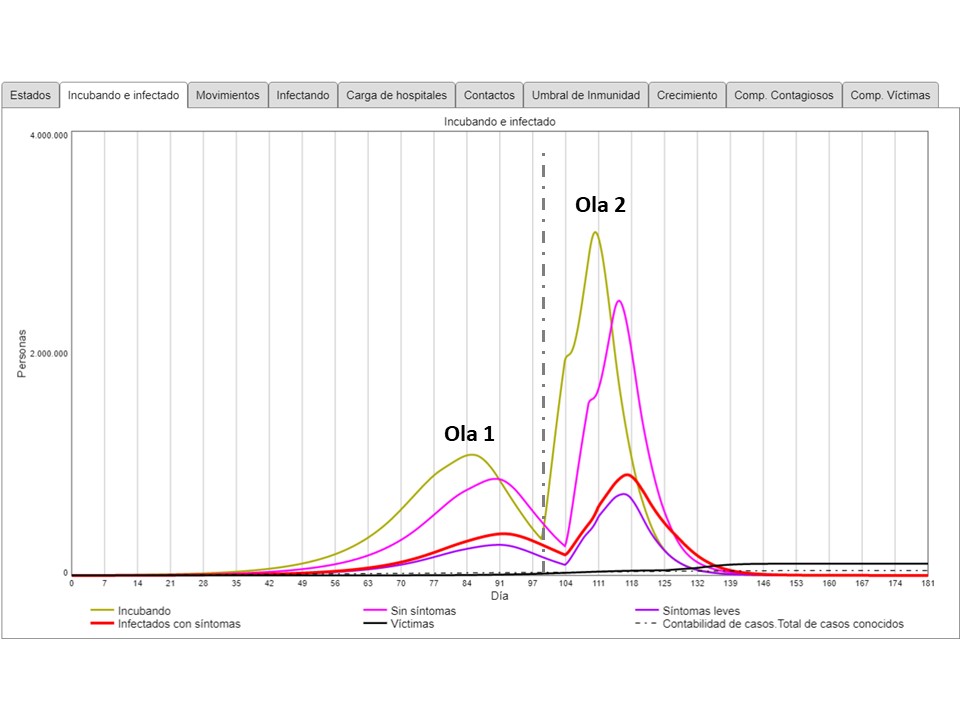
Cuando recién el número de personas incubando e infectados iba volver a niveles menos catastróficos, disparan a niveles mucho mayores que los “peak” de la primera ola. El siguiente gráfico relata claramente dos episodios de la epidemia: después de la primera semana, el “distanciamiento” genera una disminución rápida del número diario de contactos críticos de los contagiosos (en rojo). De la semana 10 u 11 en adelante, el riesgo de contagio (probabilidad que el contacto crítico de un contagioso se haga con un susceptible) baja fuertemente. A pesar del crecimiento de los contagiosos (hasta día 91), los contagios disminuyen desde el día 84.

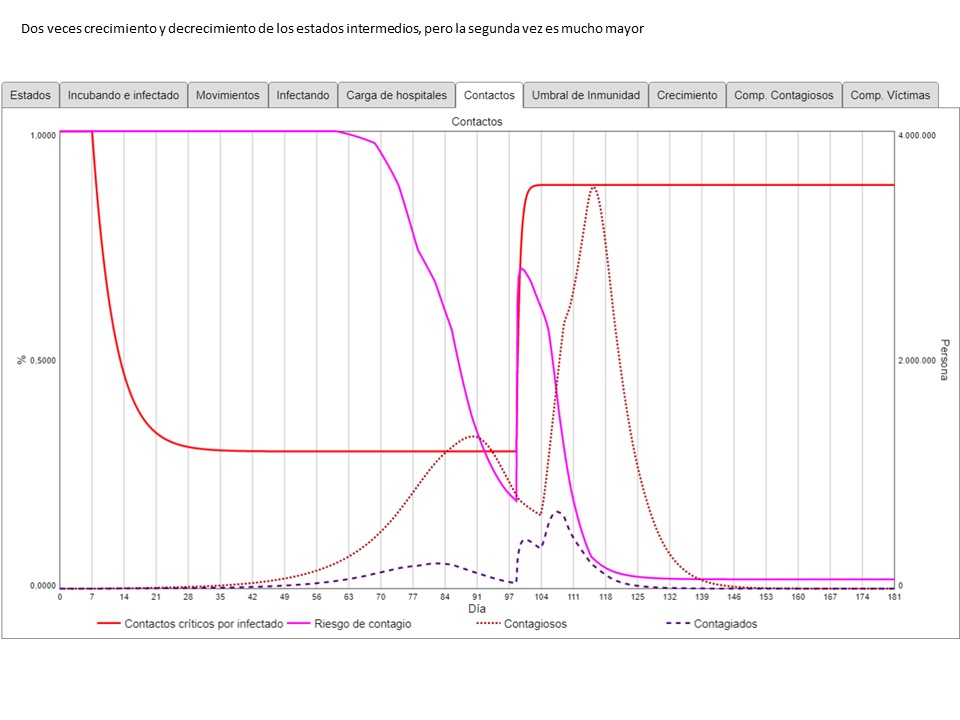
Luego se levanta el distanciammiento. El número de contactos críticos por infectado sube subitamente, y con él el riesgo de contagio – lo que debe parecer extraño, pero se explica en el párrafo siguiente. Tanto número de contagiosos como contagios crecen fuertemente, disminuyendo los susceptibles y por lo tanto el riesgo de contagio vuelve a bajar pronto, causando la vuelta a bajar de ls contagiosos y de los contagios.

Cuando cambia la tasa de contactos, cambia también el umbral de inmunidad de grupo. Este umbral representa el porcentaje de la población que debe ser inmune para que los contagiosos no logren infectar más de un susceptible, logrando así que la epidemia se hace endémica. Las dos variables tasa de contacto y umbral de inmunidad de grupo son directamente relacionadas: cuando la tasa es más elevada, un mayor porcentaje de la población debe ser inmune (lo que equivale a decir que un menor porcentaje de la población son susceptibles).

Entonces: cuando la medida de distanciamiento toma efecto, el umbral baja y la fracción que queda sano (susceptible) aumenta. En estas circunstancias, la paulatima disminución de los susceptibles (que aparece como fracción de susceptibles) genera una disminución mucho más fuerte del porcentaje normalizado de fracción de sanos – que es determinante para el riesgo de contagio (curva rosada en el gráfico anterior).

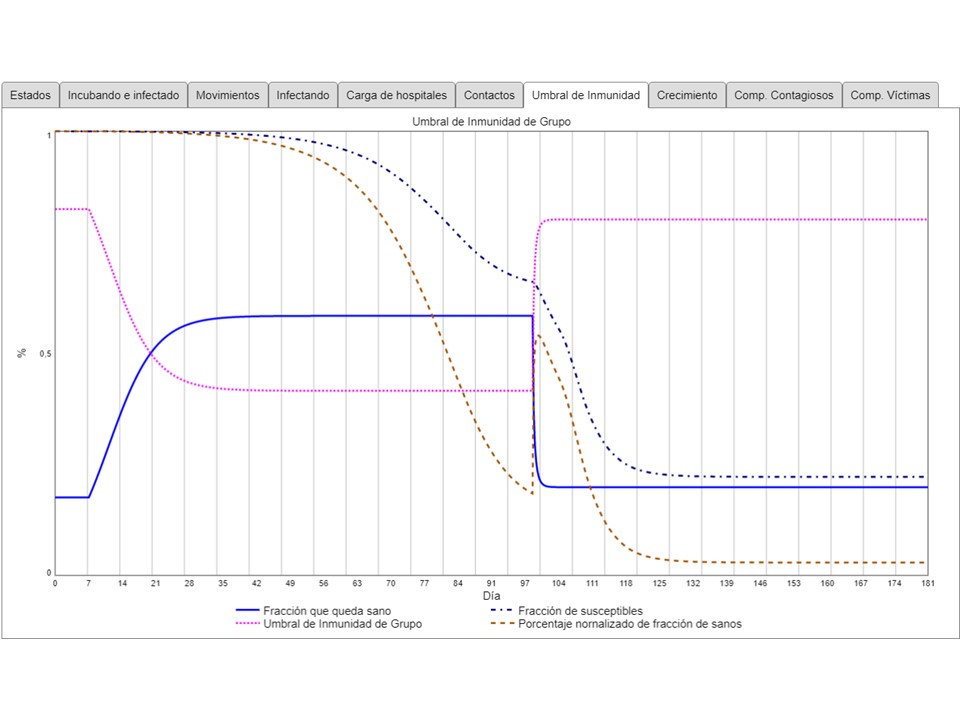
Cuando se levanta el distanciamiento, la tasa de contacto vuelve a subir muy rapidamente (la gente está contenta de volver a juntarse, esto no toma una semana), y la fracción que queda sana (por el umbral de inmunida de grupo) baja drasticamente. En estas condiciones, el porcentaje normalizado de fracción de sanos salta hacia arríba, haciendo que para el mism porcentaje de susceptibles, ahora el riesgo de contagio (gráfico anterior) será mucho más elevado. Esto da un empuje de auge a los contagios diarios, y por esta razón incubando y infectado aumentan tan fuertemente para verse como una “segunda ola”. Esto también significa que los susceptibles serán una parte pequeña de la población total, y los recuperados representarán un elevado porcentaje.

En términos de contagiosos (infectados + las personas en el útlimo día de su etapa de incubación), los tres escenarios se ven así:

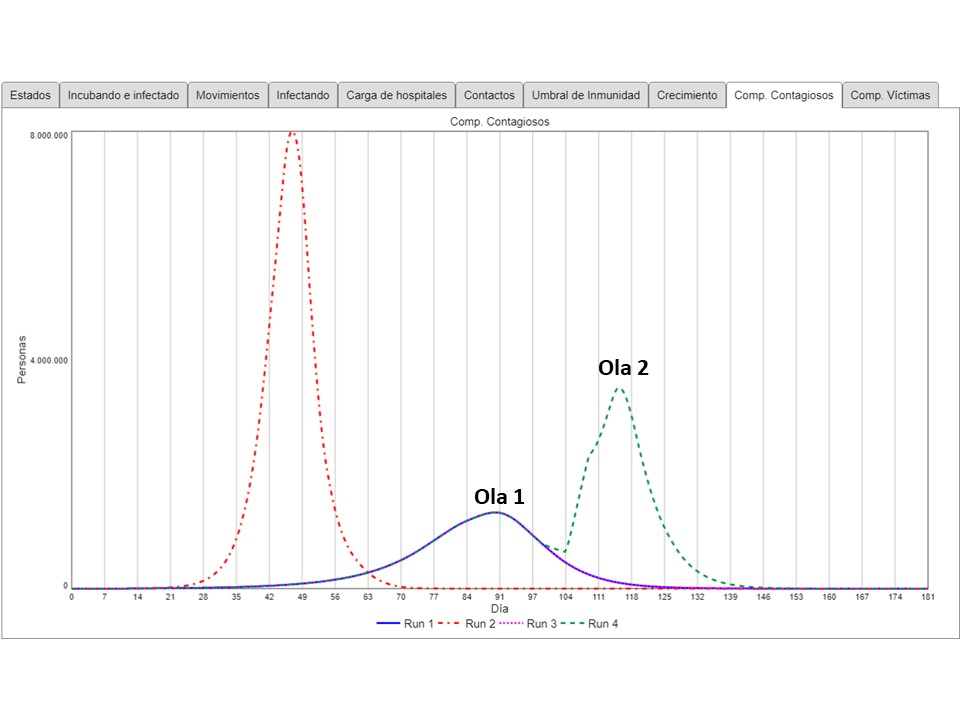
No hay peak más alto que el escenario sin distanciamiento. El distanciamiento permanente culmina 6 semanas más tarde a un nivel muy inferior. Pero cuando el distanciamento termina después de 89 días, se genera la “segunda ola” (y antes de esto no hubo “primera ola”) con un nivel a mitad de distancia entre los escenarios 1 y 2. Esto es grave porque tiene una consecuencia en términos del número total de víctimas:

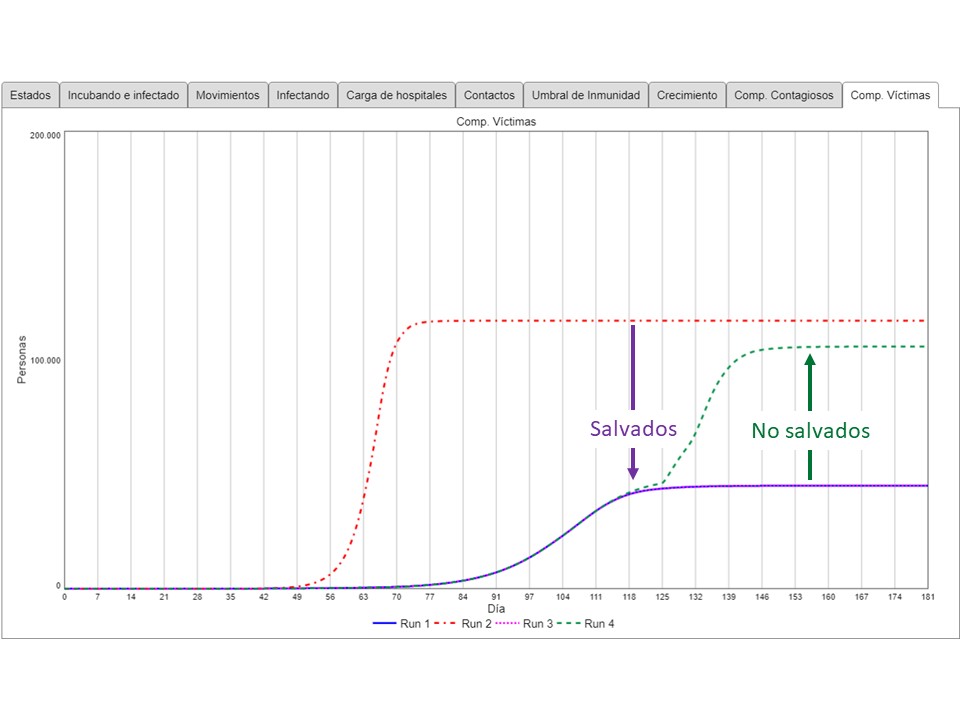
Este último gráfico muestra lo que pasaría con el número total de víctimas en los tres escenarios. Sin distanciamiento, el modelo proyecta unos 117 mil víctimas. El distanciamiento permantente (escenario 2) termina con unos 45 mil víctimas y el distanciamiento abortado el día 89 genera 105 mil víctimas. De cierto modo, levantar el distanciamiento de manera rápida conduce a no salvar las vidas de unas 60 mil personas (que se podrían haber salvado).

Ahora se ve que la segunda ola se produce porque el cambio de la tasa de contacto no es el único cambio: no se puede evitar cambiar el porcentaje de la población que deberá pasar por la infección antes de detener el proceso epidémico (el umbral de inmunidad de grupo).

Dos conclusiones me parecen indicadas:

1. el distanciamiento deberá levantarse paulatinamente – en pasos pequeños y con pausas de observación – más de esto en el próximo “post”;
2. el núnero de casos confirmados por test no será un indicador muy útil para decidir cuándo se puede empezar a reducir el distanciamiento: si vuelve a mirar los gráficos 2, 4 y 7, verá una curva negra en puntillas: son los casos reconocidos. Poder hacer alrededor de 3 mil tests por día, de los cuales la gran mayoría se aplican a personas que no tienen (en este momento) el virus, no permite a los casos reconocidos reflejar fielmente los cambios de curvatura de los casos reales (vea también el video “el desafío de los tests” y el post sobre este tema).

Por último: el modelo de simulación es muy simplificado y se basa en un gran número de supuestos (basados en estimaciones publicados por centros de investigación, que avisan de la alta incertidumbre, y que por lo tanto se transfiere también a este modelo de simulación). Vea más sobre la estructura del modelo en este video. Este modelo proyecta las consecuencias lógicas de lo poco que comprendo de lo poco que sabemos – no predice, pero me ayuda a mantener disciplina mental y transparencia – y queda a disposición de todos para examinarlo y cuestionarlo.